Mixing problems occur quite
frequently in chemical industry. We explain here how to solve the
basic model involving a single tank (see the figure on the right). The
tank contains 1000 gal of water in which initially 100 lb of salt is
dissolved. Brine runs in at a rate of 10 gal/min, and each gallon
contains 5 lb of dissolved salt. The mixture in the tank is kept
uniform by stirring. Brine runs out at 10 gal/min.
Problem
Find the amount of salt in the tank at any time t.
Background Summarize. Click here
| Outflow |
Run Rate |
10 gal/min |
| Water |
1000 |
gal |
| Salt |
100 |
lb |
| Inflow |
Run Rate |
10 gal/min |
| Salt |
5 |
lb |
Solution Step 1: Setting up a model. Click here
Let y(t) denote the amount of salt in the tank at time t. Its
time rate of change is
|
 |
|
(1) |
5 lb times 10 gal gives an inflow of 50 lb of salt. Now, the outflow
is 10 gal of brine. This is 10/1000=0.01 (=1%) of the total brine
content in the tank, hence 0.01 of the salt content y(t), that is,
0.01y(t). Thus, from (1) we obtain the following ODE as a
model:
|
 . . |
|
(2) |
Solution Step 2: Solution of the Model. Click here
The ODE (2) is separable. Separation, integration, and taking exponents on both
sides gives
Initially, the tank contains 100 lb of salt. Hence y(0)=100 is
the initial condition that will give the unique solution. Substituting
y=100 and t=0 in the last equation gives 100-5000=ce0=c. Hence
c=4900. Hence the amount of salt in the tank at time t is
|
 . . |
|
(3) |
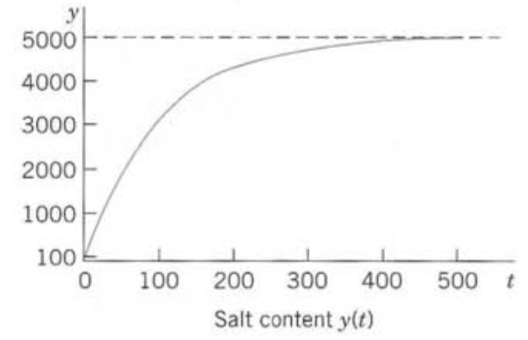
This function (see the graph
on the right) shows an exponential approach to the limit 5000 lb. Can
you explain physically that y(t) should increase with time? That its
limit is 5000 lb. Can you see the limit directly from the ODE?


 .
. ,
,  ,
,  .
. .
.