1 Heating an Office Building (Newton’s Law of Cooling)

Background

Suppose that in Winter the daytime temperature in a certain office building is maintained at 70 ∘ ⁢ F . The heating is shut off at 10 P.M. and turned on again at 6 A.M. On a certain day the temperature inside the building at 2 A.M was found to be 65 ∘ ⁢ F . The outside temperature was 50 ∘ ⁢ F at 10 P.M. and had dropped to 40 ∘ ⁢ F by 6 A.M.

Problem

What was the temperature inside the building when the heat was turned on at 6 A.M.

Physical Information

Experiments show that the time rate of change of the temperature T of a body B (which conducts heat well, as, for example, a copper ball does) is proportional to the difference between T and the temperature of the surrounding medium (Newton’s law of cooling).

Solution Step 1: Setting up a model

Let T ⁢ ( t ) be the temperature inside the building and T A the outside temperature (assumed to be constant in Newton’s Law). Then by Newton’s law,

d ⁢ T d ⁢ t = k ⁢ ( T - T A ) (1)

?

Such experimental laws are derived under idealized assumptions that rarely hold exactly. However, even if a model seems to fit the reality only poorly (as in the present case), it will still give valuable qualitative information. To see how good a model is, the engineer will collect experimental data and compare them with the calculations from the model.

Solution Step 2: General Solution

We cannot solve (1) because we do not know T A , just that it varied between 50 ∘ ⁢ F and 40 ∘ ⁢ F , so we follow the Golden Rule: If you cannot solve your problem, try to solve a simpler one.We solve (1) with the unknown function T A replaced by the average of the two known values, or 45 ∘ ⁢ F . For physical reasons we may expect that this will give us a reasonable approximate value of T at 6 A.M.

For constant T A = 45 (or any other constantvalue) the ODE (1) is separable. Separation, integration, and taking exponents gives the general solution

d ⁢ T T - 45 = k d t , ln | T - 45 | = k t + c ∗ , T ( t ) = 45 + c e k ⁢ t    ( c = e c ∗ )

Solution Step 3: Particular Solution

We choose 10 P.M. to be t = 0 . Then the given initial condition is T ⁢ ( 0 ) = 70 and yields a particular solution, call it T p . By substitution

T ⁢ ( 0 ) = 45 + c ⁢ e 0 = 70 , c = 70 - 45 = 25 , T p ⁢ ( t ) = 45 + 25 ⁢ e k ⁢ t .

Solution Step 4: Determination of k

We use T ⁢ ( 4 ) = 65 , where t = 4 is 2 A.M. Solving algebraically for k and inserting k into T p ⁢ ( t ) gives (see Figure LABEL:fig:temp)

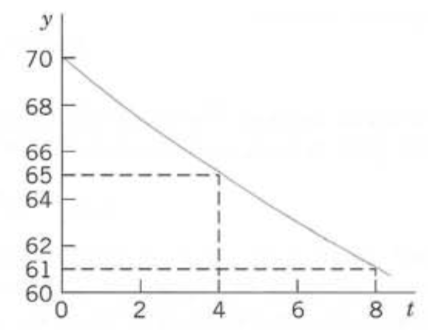T p ⁢ ( 4 ) = 45 + 25 ⁢ e 4 ⁢ k = 65 , e 4 ⁢ k = 0.8 , k = 1 4 ⁢ ln ⁡ 0.8 = - 0.056 , T P ⁢ ( t ) = 45 + 25 ⁢ e - 0.056 ⁢ t .
Figure 1: Particular Solution (temperature)

Solution Step 4: Answer and Interpretation

6 A.M. is t = 8 (namely 8 hours after 10 P.M.), and

T p ⁢ ( 8 ) = 45 + 25 ⁢ e - 0.056 ⋅ 8 = 61 .

Hence the temperature in the building dropped by 9 ∘ ⁢ F from 70 ∘ ⁢ F to 61 ∘ ⁢ F , a result that looks reasonable.

Lead vocal of Gfriend.

Details about the formula (to be coming soon)
The temperature at which water freezes into ice is defined as 32 ∘ ⁢ F or 0 ∘ ⁢ C